Творческие работы по Физике 2 (Mr. Jones.)

Задача №1
Проекция скорости Мистера изменяется по закону vx=20+5t
- определите характер движения Мистера
- найти величину и направление начальной скорости
- найти проекцию ускорения, величину и его направление
- определить скорость Мистера через 3 секунды
- построить график зависимости ускорения от времени

Решение:
Уравнение движения при равноускоренном движении:
vx=v0x+at
Данное уравнение:
vx=20+5t
Отсюда следует =>
V0x=20 m/c
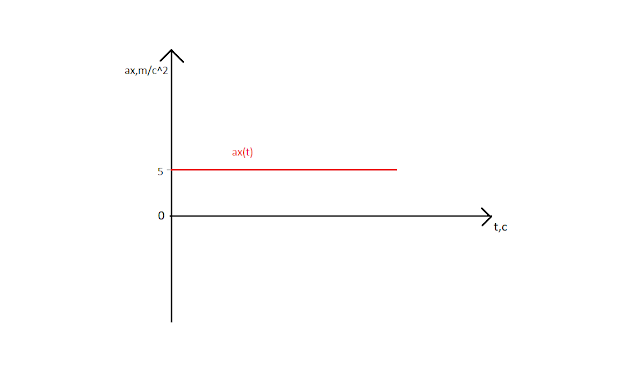
ax=5 m/c^2

Найдём скорость Мистера через 3 секунды:
Vx=20+5*3=35 m/c
Рисунок:

Построим график зависимости ускорения от времени:
 

Ответ:
Vx=20 m/c
ax=5 m/c^2
при t=3c Vx=35 m/c 
характер движения- равноускоренное 

Задача №2 
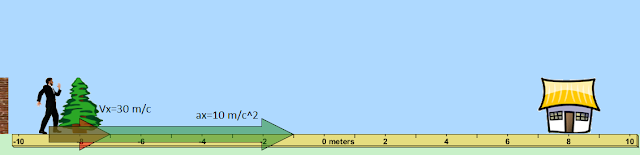
Когда Мистер гулял по саду, ему позвонила жена и сказала, что в доме дверь захлопнулась, и остался включенный утюг, а ключи были только у Мистера.Он помчался домой со скорость 30 м/с и прибавил ускорения 10 м/с^2
- составте уравнение движения   
- опишите характер движения
- постройте график зависимости скорости от времени
  
Решение:

 Характер движения- равноускоренное,
запишем уравнение движения при равноускоренном движении:Vx=V0x+at
 отсюда следует:
Vx=30+10t 
Построим график зависимости скорости от времени:

Ответ:
Vx=30+10t
Характер движения- равноускоренное 


Задача №3 
Мистер решил погулять по лесу, но как только он туда вошёл, ему повстречался злобный волк, Мистер побежал домой с ускорением 3 м/с^2 и добежал до дома за 10 секунд, у дома скорость была равна 15 м/с.
- определите первоначальную скорость Мистера
- постройте график зависимости ускорения от времени

Решение:

  Запишем уравнение движения при равноускоренном движении:
Vx=V0x+at
Подставив данные , вычислим начальную скорость:
15=V0x+3*10
15=V0x+30
V0x=-15 m/c


Построим график зависимости ускорения от времени:

 Ответ:
V0x=-15 m/c

Творческие работы по Физике (Mr. Jones.)

Задача №1
На рисунке показан Mr. Jones.
- описать характер движения Mr. Jones по данным рисунка
- составить уравнение движение Mr. Jones при равномерном движении
- найти в какой момент времени Mr. Jones пройдёт мимо своего дома, если его координата равна xa=8

Рисунок 1

Решение:
Запишем уравнение движения тела при равномерном движении в общем виде:
x=x0+Vxt
По рисунку видно, что:
x0=-4
Vx=10 м/с
=> Запишем уравнение:
x=-4+10t
Теперь найдём в какой момент времени Мистер будет проходить дом:
xa=8
ta-?
8=-4+10t
10t=12
t=1,2(с)
Наглядный пример:

Рисунок 2

Ответ:
x=-4+10t
ta=1,2(с)



Задача №2
Движение двух братьев-близнецов Mr. и Mr. Jones описывается уравнениями:
- x1=6-2,5t
- x2=-6+4t
  - найти начальные координаты тел
  - величины и направление векторов скорости
  - место и время встречи братьев Jones
 Решение:
1 брат:                                                                         2 брат:
x0=6                                                                              x0= -6
Vx=-2,5 m/c                                                                  Vx=4 m/c
Встреча: 
x1=x2
6-2,5t=-6+4t
12=6,5t
t=1,8(c)

Место:
 x2=-6+4t=-6+4*1,8=-6+7,2=1,2

Рисунок:

Рисунок к задаче

Ответ:
1 брат:
x0=6
Vx=-2.5 m/c

2 брат:
x0=-6
Vx=4 m/c

Встреча :
t=1,8 с
x=1,2 


Задача №3
По прямой дороге в одном направлении двигаются Mr. Jones  и мяч. Скорость Мистера равна 20 м/с, мяч догоняет его со скоростью 30 м/с.Расстояние между ними равно 2 м.

- написать уравнения движения Мистера и мяча( приняв за начало координат место нахождения мяча в начальный момент времени и выбрав за положительное направление оси х направление движения Мистера и мяча.)
- найти место и время их встречи 
- построить графики зависимости V(t)и х(t)

Решение:
Для решения задачи, нарисуем рисунок:

Рисунок к задаче

 
Теперь нам будет легче написать уравнения движения:
Рассмотрим Мистера:                                                    Рассмотрим мяч:
x=x0+Vxt                                                                           x=x0+Vxt
x1=2+20t                                                                            x=30t


Теперь мы можем найти место и время встречи Мистера и мяча(т.к. мяч догоняет Мистера):
Встреча:
x1=x2
2+20t=30t
2=30t-20t
2=10t
t=0,2(с)
Место:
x2=30t=30*0,2=6

График зависимости координаты от времени:

График

График зависимости скорости от времени:

График

  Ответ: 
Мистер: x=2+20t
Мяч: x=30t
Встреча: место и время: t=0,2 c, x=6

Творческие работы по Физике (Задание 2) Вариант 6

              "Определение проекций вектора на оси"

Вариант №6

Цель:

• определить координаты начало и конца каждого вектора
• определить проекции  векторов на оси
• определить длину векторов
• определить сумму и разность двух предложенных векторов 

     

        

              Результаты вычислений:

Вектор AB:

Начальные координаты:                   Конечные координаты:

x₀= -6                                                                x=1
y₀= 11                                                                y=3                         

Проекции векторов:

Sx=x-x₀                Sy=y-y₀

Sx=1-(-6)=1+6=7      Sy=3-11=-8

                                      
Длина вектора AB: 
(по модулю)S ² =Sx²+Sy²

(по модулю)S²=49+64=113

Вектор CD:

Начальные координаты:                          Конечные координаты:

x₀=6                                                                               x=8

y₀= 6                                                                              y=11
Проекции векторов:

Sx=x-x₀          Sy=y-y₀

Sx=8-6=2      Sy=11-6=5

                                    
Длина вектора CD:

 (по модулю) S²=Sx²+Sy²

 (по модулю)S²=4+25=29

                                         Сумма AB+CD:

Переместим векторы так, чтобы начальная точка CD лежала в конечной точке AB:

AB+CD=AD

Вектор AD

A( -6,11)

D(3,11)

Sx=x-x₀                                   Sy=y-y₀

Sx=3-(-6)=3+6=9            Sy=11-11=0

(по модулю)AD²=Sx²+Sy²

(по модулю)AD²=81+0=81=9

AD=9

                                      Разность AB-CD:

Переместим векторы так, чтобы оба вектора AB и CD выходили из одной точки:

AB-CD=BD

Вектор BD

B(1,3)

          D(-4,16)

Sx=x-x₀                            Sy=y-y₀ 
Sx=-4-1=-5                Sy=16-3=13

BD²⁼Sx²+Sy²

      (по модулю)BD²=25+169=194

      (по модулю)BD=194

Творческие работы по Физике(БК)

                                               Определение перемещения БК

                               Отчёт о проделанной работе:
Цель работы:
Определить проекции перемещения и величины самого перемещения БК,
Сравнить пути и перемещение БК.
1 вариант:

                                                  Результаты измерений:
Начальные координаты:                                                                  Конечные координаты:

y₀ = 6                                                               x=13

x₀= 5                                                                y= -3

Проекции перемещения: 
Sx= x-x₀       Sx= 13-6=7

Sy= y-y₀       Sy=-3-5= -8

Длина перемещения: 
(по модулю) Sx  ² = Sx²+Sy² 
(по модулю)Sx  ² =49+64=113=10,6

Сравнение: Путь и перемещение 
Путь и перемещение не равны

Ø   Путь-величина скалярная

Ø   Перемещение - векторная

      




                                                     Определение перемещения БК 
                                    Отчёт о проделанной работе  
                                  Вариант 2                
Цел.

                                                       Результаты измерений:
                     Начальные координаты:                                                            Конечные координаты: 

                      x0=60                                                  x=-20                                                                 y0=19                                                  y=30

                                                                          

        Проекции перемещения:

          Sx= x-x₀       Sx= -20-60=-80

          Sy= y-y₀       Sy=30-19=11

         Длина перемещения:
        (по модулю)Sx  ² = Sx²+Sy²

       (по модулю)Sx  ² =6400+121=6521=80.75

        Сравнение: Путь  и перемещение:
        Путь и перемещение не равны(это видно по графику)
            Путь величина-скалярная
             Перемещение - векторная 

                                        



                                                     Определение перемещения БК 
                                    Отчёт о проделанной работе: 
                      Вариант 3                
Цел.

                                                     Результаты измерений:
                      Начальные координаты:                                                                   Конечные координаты: 
                       x0=-10                                                        x=25                                                       y0=5                                                         y=-30
                                                                          

        Проекции перемещения:

          Sx= x-x₀       Sx= 25-(-10)=35

          Sy= y-y₀       Sy=-30-5=-35

          Длина перемещения:
        (по модулю)Sx  ² = Sx²+Sy²

       (по модулю)Sx  ² =1225+1225=2450=49,5

        Сравнение: Путь  и перемещение:
        Путь и перемещение не равны(это видно по графику)
            Путь величина-скалярная
            Перемещение - векторная 

                                                           

C Днём Знаний!