МКТ(облако слов)

Домашнее задание № 5. Работа с графическими моделями.Статика.

Задача №3:

К концам подоконника длиной 12 см приложены две силы 20 и 10 H.Пренебрегая весом подоконника, определить, где надо подпереть балку, чтобы она находилась в равновесии? Дайте ответ в метрах, от точки приложения меньшей силы.

Решение:
1)Нам требуется найти х, т.к. F2- точка приложения меньшей силы.
12 cм=0,12м
2) По II условию равновесия EM=0
( алгебраическая сумма моментов)
MF1+MF2+MN=0
3) ось вращения - точка О => MN=0

4)О:MF1-MF2=0
MF1=MF2
5)F1*(l-x)=F2*x
6)20 H *(0,12-x)=10 H*x
2,4-20x=10x
2,4=10x+20x
2,4=30x
x=0,08 м


Ответ: 0,08 м от точки приложения меньшей силы.

Домашнее задание № 5. Работа с графическими моделями.Статика.

Задача №2:

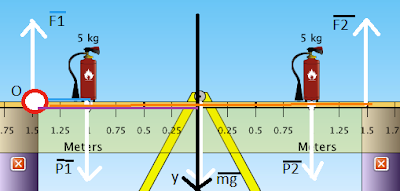
Однородная балка длиной 10 м, весящая 620 Н, поддерживается двумя столбцами(опорами), расположенными у её концов. На балке стоят два груза, одинаковым весом 50 H , и оба находятся на расстоянии 1 м от левого и правого конца балки. Чему равны силы, с которыми опоры действуют на балку?

Решение:
1) Нарисуем рисунок, обозначим силы, выберем ось вращения => будем начинать своё II условию равновесия.

2) По II условию равновесия EM=0(алгебраическая сумма)
MF1+MF2+MP1+MP2+Mmg=0
Берём за ось вращения точку О => МF1=0
3)O: -MF2+Mmg+MP1+MP2=0
4)F2= (mg*Lmg)+(P1*Lp1)+(P2*Lp2) / Lf2
5) F2= 360H
6) Теперь найдём  силу F1:
 По I условию равновесия  EF=0
(геометрическая сумма сил)
7)oy: P1+P2+mg-F1-F2=0
8)F1=mg+P2+P1-F2=620H+50H+50H-360H=360 H

Ответ: F1=F2=360H

Домашнее задание № 5. Работа с графическими моделями.Статика.

Задача №1

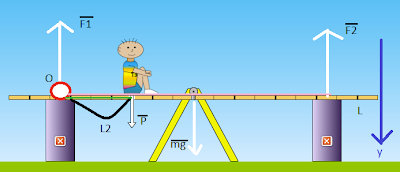
Стол длиной 500 см( от опор) и массой 120 кг стоит на двух опорах-ножках стола. На столе сидит непослушный мальчик весом 20Н, на расстоянии 2 м от левого конца стола.Определите силы, с которыми опоры действуют на стол?

Решение:
1) Сначала переведём см в м, т.к. мы работаем в системе СИ: 500см=5 м
2) Рисуем рисунок, показываем силы, выбираем ось вращения => решаем по II условию равновесия.

3) Берём за точку вращения точку О
4) Нам требуется найти силу F1 и силу F2
5)По II условию равновесия
(алгебраическая сумма) EM=0
МF1+MF2+MP+Mmg=0
MF1=0. т.к. о- ось вращения
6)О: -МF2+MP+Mmg=0


7) -(F2*Lf2)+(P*Lp)+(mg*Lmg)=0
        -(F2*5 м)+(20H*2 м)+((120кг*10 м/c^2) *2,5м)=0
        -(F2*5м)+3040=0
        -(F2*5 м)=-3040
          F2=-3040/-5=608 H
    8) Далее, по I условия равновесия найдём F1:
   EF=0 (геометрическая сумма)
   oy: P+mg-F1-F2=0
   P+mg-F2=F1
   F1=20H+(120кг*10 м/с^2)-608Н=612 Н

Ответ: F1=612H; F2=608H.